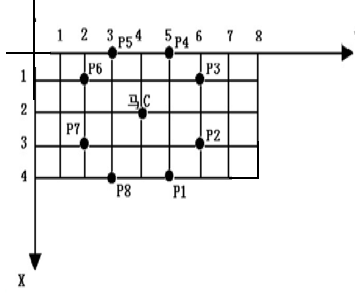
我们都知道象棋中马走”日”,比如在 (2, 4)(2,4) 位置的一个马,跳一步能到达的位置有 (0, 3)(0,3),(0, 5)(0,5),(1, 2)(1,2),(1, 6)(1,6),(3, 2)(3,2),(3, 6)(3,6),(4, 3)(4,3),(4, 5)(4,5)。
蒜头君正在和花椰妹下棋,蒜头君正在进行战略布局,他需要把在 (x,y)(x,y) 位置的马跳到 (x’, y’)(x′,y′) 位置,以达到威慑的目的。
但是棋盘大小有限制,棋盘是一个 10×9 的网格,左上角坐标为 (0, 0)(0,0),右下角坐标为 (9, 8)(9,8),马不能走出棋盘,并且有些地方已经有了棋子,马也不能跳到有棋子的点。
蒜头君想知道,在不移动其他棋子的情况下,能否完成他的战略目标。
输入格式
输入一共 10 行,每行一个长度为 9 的字符串。
输入表示这个棋盘,我们用'.'表示空位置,用'#'表示该位置有棋子,用'S'表示初始的马的位置,用'T'表示马需要跳到的位置。
输入保证一定只存在一个'S'和一个'T'。
输出格式
如果在不移动其他棋子的情况下,马能从'S'跳到'T',那么输出一行"Yes",否则输出一行"No"。
样例输入复制
.#....#S# ..#.#.#.. ..##.#..# ......##. ...T..... ...#.#... ...#..... ...###... ......... .##......
样例输出复制
Yes
标程题解
#include <iostream>
using namespace std;
//存储地图的数组
char s[10][9];
//记录是否被访问过
bool vis[10][9];
//方向偏移量数组
int dir[8][2] = {{2,1},{1,2},{-1,2},{-2,1},{-2,-1},{-1,-2},{1,-2},{2,-1}};
//判断是否在范围内的函数
bool in(int x, int y) {
return x >= 0 && x < 10 && y >= 0 && y < 9;
}
//深度优先搜索的递归函数
bool dfs(int x, int y) {
vis[x][y] = true;
if (s[x][y] == 'T') {
return true;
}
for (int i = 0; i < 8; i++) {
int tx = x + dir[i][0];
int ty = y + dir[i][1];
if (in(tx, ty) && !vis[tx][ty] && s[tx][ty] != '#') {
if (dfs(tx, ty)) {
return true;
}
}
}
return false;
}
//主函数
int main() {
int x, y;
//读入地图
for (int i = 0; i < 10; i++) {
cin >> s[i];
}
//找到起点位置
for (int i = 0; i < 10; i++) {
for (int j = 0; j < 10; j++) {
if (s[i][j] == 'S') {
x = i;
y = j;
}
}
}
//将起点位置输入dfs函数,开始搜索
if (dfs(x, y)) {
cout << "Yes" << endl;
} else {
cout << "No" << endl;
}
return 0;
}